Site menu:

Sprache auf englisch umschalten

cNORM - Troubleshooting und Rarely Asked Questions


Inhalt

  1. Perzentillinien überschneiden sich
  2. Benötigte Stichprobengröße
  3. Geringer Zusammenhang zwischen explantorischer Variable und Rohwerten
  4. Stark wellige Perzentillinien
  5. Modellierung mit einer kontinuierlichen Altersvariablen klappt nicht
  6. Können Fälle der Normierungsstichprobe gewichtet werden?


cNORM funktioniert in vielen Anwendungsszenarien "out of the box", v. a. bei einer hinreichend großen Datenmenge und wenn der Zusammenhang zwischen der explanatorischen Variable und den Rohwerten groß genug ist (also beispielsweise bei einem deutlichen Alterstrend). Es gibt jedoch auch Fälle, die schwieriger zu handhaben sind. Wir raten in jedem Fall dazu, die generierten Lösungen auf Plausibilität zu prüfen und die Parameter falls nötig "manuell" nachzujustieren. Ähnlich wie bei Faktorenanalysen ist die Modellauswahl ein mehrstufiger Prozess, bei dem i. d. R. verschiedene Modelle durchgerechnet und hinsichtlich unterschiedlicher Gütekriterien miteinander verglichen werden müssen. Im Fall von cNorm gibt es vor allem drei Gütekriterien, nämlich die Varianzaufklärung, die Einfachheit des Modells sowie die Modellplausiblität bzw. -konsistenz. Letztere muss in der Regel vor allem an den Modellrändern beachtet werden.

Kurz zusammengefasst:

  1. Powerparameter von k = 5 für die Personenlokation und t = 3 für das Alter sind für fast alle Anwendungszwecke ausreichend. Wenn mit diskreten Gruppen gearbeitet wird, dann sollte der Parameter t immer mindestens 1 niedriger als die Anzahl an Gruppen gewählt werden. Wenn beispielsweise nur zwei Altersgruppen vorliegen, dann sollte t nur auf 1 gesetzt werden, da höhere Zusammenhänge in diesem Fall nicht erfasst werden können.
  2. Modelle mit einer relativ geringen Anzahl an Termen (z. B. 'terms = 4' bis 'terms = 10') sind häufig am robustesten und erbringen in Kreuzvalidierungen in der Regel die besten Ergebnisse. Vermeiden Sie Modelle mit vielen Termen und nehmen Sie stattdessen lieber ein etwas geringeres R2 in Kauf.
  3. Inspizieren Sie nach einer ersten Modellberechnung die Informationsfunktionen ('plotSubset()') und Perzentildiagramme ('plotPercentiles()' und 'plotPercentileSeries()') in Abhängigkeit von der Anzahl der Prädiktoren. Berechnen sie zuletzt noch einmal das Modell mit denjenigen Parametern, die Sie zuvor als optimal bestimmt haben, also z. B. mit einer bestimmten Anzahl an Termen.
  4. Egal ob Sie diskrete Altersgruppen oder ein 'sliding window' verwenden: Die Intervallbreiten sollten immer so gewählt werden, dass mindestens 100 Personen pro Gruppe bzw. pro sliding window enthalten sind. Bei einem Datensatz mit vielen fein abgestuften Altersgruppen mit kleinen Stichproben kann es deshalb günstiger sein, die Altersgruppen zu breiteren Intervallen zusammenzulegen.



1. Perzentillinien überschneiden sich

Bei der Modellierung kann es v. a. in den Extrembereichen oder bei starken Boden- oder Deckeneffekten zu inkonsistenten Modellen kommen. Diese äußern sich beispielsweise darin, dass sich die Linien der Perzentile überschneiden ('plotPercentiles()') bzw. dass bei der Modellierung eine entsprechende Warnung ausgegeben wird ('checkConsistency()'). Seit der Version cNORM 3.2 sind in der 'cnorm()'-Funktion zwar automatische Checks eingebaut, die dafür sorgen sollen, dass möglichst keine Modelle mit Inkonsistenzen zurückgeliefert werden. Es handelt sich dabei aber nur um grobe Überprüfungen. Im Einzelfall können also trotzdem noch Perzentillinien auftreten, die sich überschneiden.

Mögliche Lösungen:

# Stellt ein Perzentildiagramm des aktuellen Modells dar

plotPercentiles(model, data)

# Erzeugt eine Serie an Perzentildiagrammen mit bis zu 10 Termen

plotPercentileSeries(model, data, end=10)



2. Benötigte Stichprobengröße

Unsere Simulationen weisen darauf hin, dass bereits ab einer Gruppengröße von 50 Fällen pro Altersgruppe relativ reliable Modelle berechnet werden können (siehe Abbildung). Trotzdem empfehlen wir, die Stichprobengröße von 100 pro Altersgruppe (bwz. beim 'sliding window' pro Breite des Fensters) nicht zu unterschreiten. Dies liegt vor allem daran, dass die Repräsentativität der Normierungsstichprobe einen wichtigen Einflussfaktor darstellt. Diese herzustellen, ist bei Gruppengrößen mit weniger als 100 Personen oft schwierig. Denn wenn die Fallzahl zu klein gewählt wird, dann reduziert sich nicht nur die Power der angewandten statistischen Verfahren, sondern es wird auch schwierig, die Stichprobe hinsichtlich aller relevanten Merkmale zu stratifizieren.


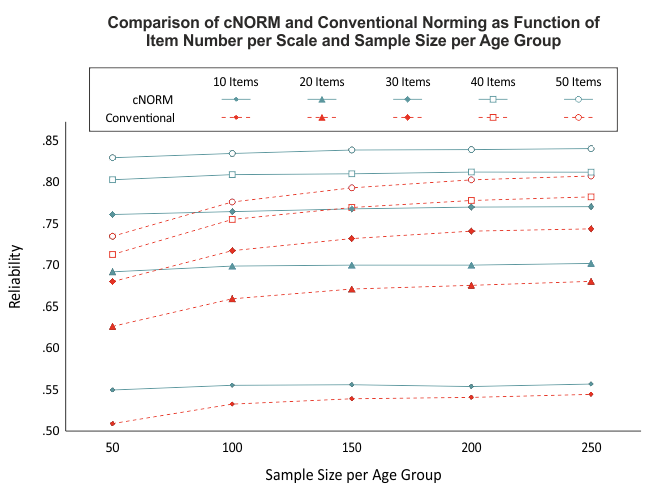
Comparison of cNORM and Conventional Norming in Dependence of Number of Items per Scale and Sample Size per Age Group

cNORM ist zwar in der Lage, kleinere Verletzungen der Repräsentativität oder geringe Fallzahlen in einzelnen Altersgruppen teilweise zu kompensieren, da die Modelle auf der Basis des gesamten Datensatzes berechnet werden. Dennoch sollte bei der Normierung eines Testverfahrens auf eine sehr hochwertige Datengrundlage geachtet werden.

Mögliche Lösung:



3. Geringer Zusammenhang zwischen explantorischer Variable und Rohwerten

Seit Version 1.1.8 prüft cNORM automatisch mittels polynomialer Regression, welcher Anteil der Varianz der Rohwerte durch die explanatorische Variable erklärt wird. Liegt nur ein kleiner Zusammenhang zwischen der explanatorischen Variablen und den Rohwerten vor, so wirft cNORM eine Warnmeldung aus. Es stellt sich in diesem Fall die Frage, ob der Einbezug der explanatorischen Variablen in die Berechnung der Normen wirklich sinnvoll ist oder ob nicht beispielsweise eine einzelne Normtabelle ausreicht. Bei einer niedrigen Varianzaufklärung der explanatorischen Variablen kann es bisweilen vorkommen, dass die Modelle nicht sehr stabil sind und dass die angestrebte Varianzaufklärung des Gesamtmodells von R2 ≥ .99 nicht erreicht wird.

Mögliche Lösungen:



4. Stark wellige Perzentillinien

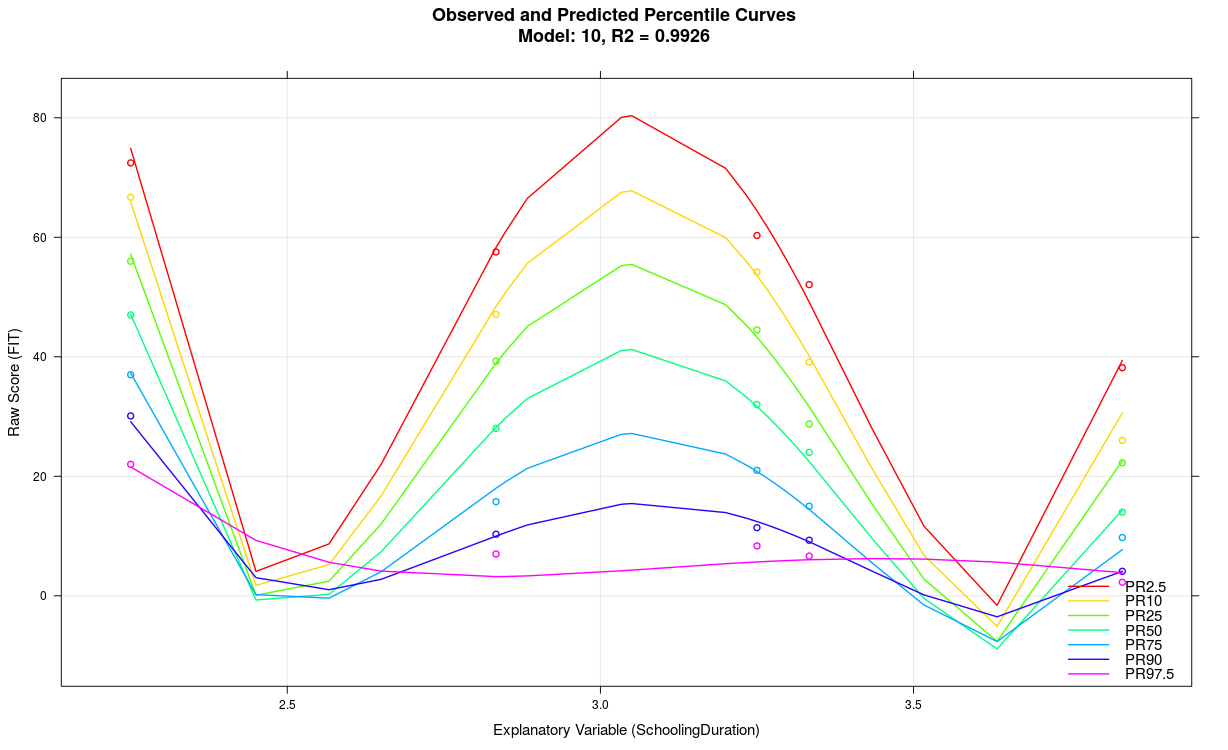
Mögliche Überanpassung

Das Modell weist wahrscheinlich einen Overfit auf, z. B. weil der Parameter 't' zu hoch gewählt wurde, die Varianzaufklärung der explanatorischen Variable nicht sehr hoch ist, zu viele Prädiktoren verwendet wurden, die Skala generell nicht reliabel misst, usw.. Es kann auch eine Folge zu kleiner Fallzahlen in den einzelnen Gruppen sein, wie z. B. im obigen Beispiel mit n = 50. Möglicherweise kommt das cNORM-Package im konkreten Fall auch an die Grenze seiner Leistungsfähigkeit. Meistens empfiehlt es sich, ein einfacher strukturiertes Modell mit weniger Termen zu verwenden.

Mögliche Lösungen:

Im obigen Beispiel war der Parameter 't' bei einer Gruppengröße von nur 50 auf t = 5 gesetzt. Setzt man den Parameter auf t = 3 und reduziert gleichzeitig die Anzahl an Termen von 21 auf nur 7, ergibt sich folgendes Model:


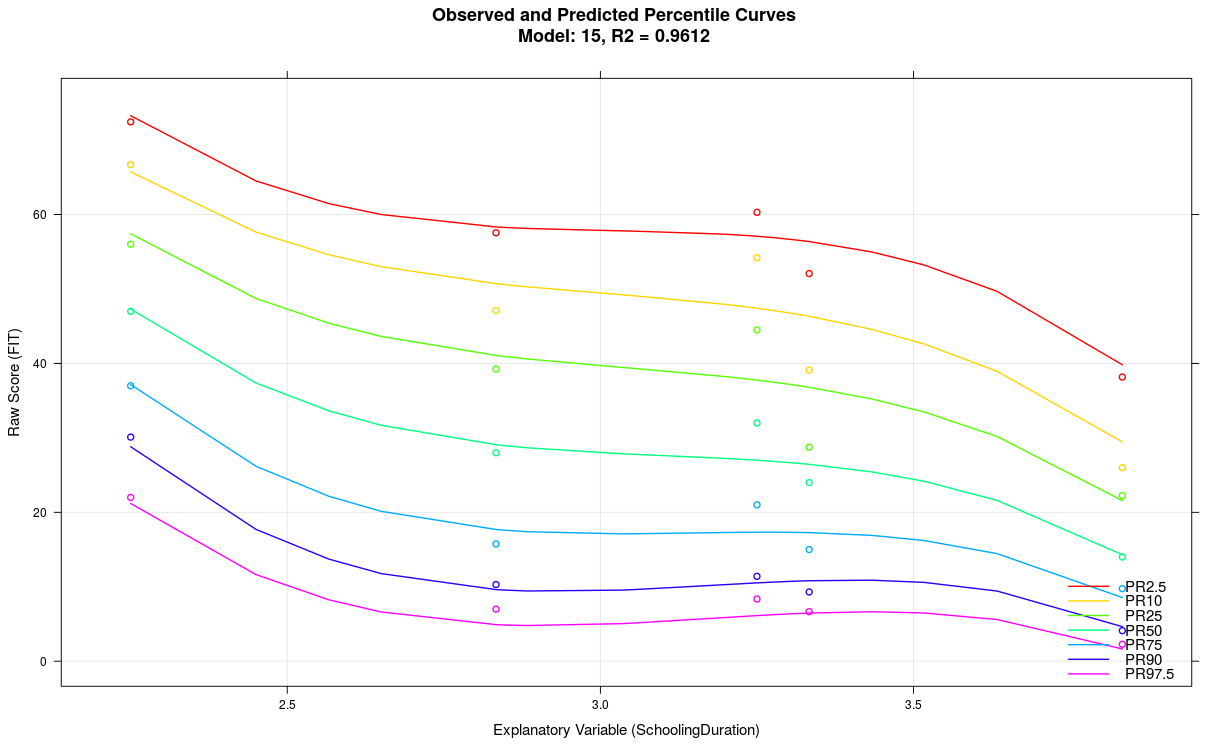
Vermeidung einer Überanpassung


5. Modellierung mit einer kontinuierlichen Altersvariablen klappt nicht

Verwenden Sie stattdessen diskrete Altersgruppen. Wenn Sie in der 'cnorm()'-Funktion eine Gruppierungsvariable spezifizieren, dann wird das Ranking mittels dieser Gruppierungsvariable vorgenommen. Damit die Modellierung funktionieren kann, muss allerdings die Gruppierungsvariable mit der Altersvariablen korrespondieren. Das bedeutet: Die Werte der Gruppierungsvariablen sollten das mittlere Alter der jeweiligen Altersgruppe wiederspiegeln.

Mögliche Lösungen:

# Erzeugt aus einer kontinuierlichen Altersvariable eine
# Gruppierungsvariable mit 10 gleichgroßen Gruppen

ADHD$group <- getGroups(ADHD$age, n = 10)



6. Können Fälle der Normierungsstichprobe gewichtet werden?

Mit dem Parameter 'weights' kann eine Gewichtung der Fälle vorgenommen werden. cNORM beinhaltet mit 'computeWeights()' außerdem eine Funktion zur Erzeugung von Gewichten mit Hilfe von Raking. Hierdurch kann der Effekt unbalancierter Normstichproben reduziert werden.



Jamovi
 Überblick