Site menu:

Verteilungsfreie Modellierung mit cNORM - Mathematischer Hintergrund
Bei dem von uns verwendeten mathematischen Ansatz wird der Rohwert r einer Testskala als kontinuierliche Funktion des latenten Personenparameters l und einer explanatorischen Variable a modelliert.
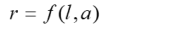
Verwendete Parameter
Der Personenparameter l ist dabei die Lokation der Person in Bezug auf andere Personen der Bezugsgruppe. Als Bezugsgruppe werden dabei alle Personen der betreffenden Population verstanden, die hinsichtlich der explanatorischen Variable a die gleiche Ausprägung haben. Für einen Intelligenztest, der Gültigkeit im deutschsprachigen Raum besitzen soll, wären dies also z. B. alle Kinder des gleichen Alters, die in Deutschland, Österreich oder der deutschsprachigen Schweiz leben. Die Lokation l kann als Rangplatz (= Perzentil) oder als standardisierter Normwert ausgedrückt werden. Da die wahre Lokation zunächst noch unbekannt ist, startet die verteilungsfreie Modellierung in cNORM mit der Bildung konventioneller Gruppen (also z. B. Altersgruppen). Die Lokation wird dann zunächst einmal durch eine Normalrangtransformation aus dem jeweiligen Perzentil innerhalb der Gruppe geschätzt.
Verwendet man standardisierte Normwerte, dann liegt diesem Vorgehen im Prinzip die implizite Annahme zugrunde, dass der zu messende latente Personenparameter in der Bevölkerung normalverteilt ist. Dies trifft auf viele, aber nicht auf alle psychologischen oder physiologischen Parameter zu. So ist beispielsweise ein physiologischer Parameter wie der Body-Mass-Index rechtsschief verteilt. Trotzdem lassen sich solche Größen sehr gut mit Hilfe des in cNORM implementierten verteilungsfreien Ansatzes modellieren. Allerdings sollte man die resultierenden Normwerte bei Maßen wie dem Body-Mass-Index am Ende wieder in Perzentile umwandeln.
Die explanatorische Variable a ist eine Variable, die systematisch mit der zu messenden Größe oder Leistung kovariiert. So steigt beispielsweise die absolute Fähigkeit zum logischen Denken im Kindes- und Jugendalter monoton an. Die explanatorische Variable wäre in diesem Fall also das Alter. Andere Leistungen hängen eher davon ab, wie lange ein Kind beschult wurde. Die explanatorische Variable wäre dann die Beschulungsdauer. Auch dichotome Variablen (z. B. Geschlecht) können theoretisch als explanatorische Variablen herangezogen werden.
Mathematische Herleitung
Zwar stellen Rohwerte bei den meisten psychometrischen Testverfahren ganzzahlige Werte dar. Zur mathematischen Herleitung kann den diskreten Werten allerdings ein Kontinuum unterlegt werden. In diesem Fall liegt im Messbereich des Tests eine glatte Funktion vor, die in der Regel beliebig oft differenziert werden kann. Für solche Funktionen gilt, dass sie an einem beliebigen Punkt P(l0, a0) auch als sogenannte Taylorreihe geschrieben werden können:
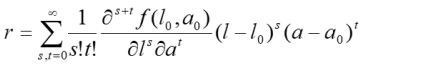
Solche Taylorreihen konvergieren zwar normalerweise nur innerhalb eines bestimmten Radius um den Punkt P gegen die zu modellierende Funktion. In der Praxis hat sich aber erwiesen, dass man viele Funktionen über einen ausreichenden Radius hinweg damit extrem gut nähern kann, z. B. die Daten psychologischer oder physiologischer Testverfahren.
Da das Taylorpolynom eine unendliche Summe darstellt, kann diese Summe nur dann gegen einen endlichen Wert konvergieren, wenn die einzelnen Summanden mit steigendem s und t sehr schnell sehr klein werden. Dies bedeutet gleichzeitig, dass bei großem s und t die Summanden nur noch einen geringen Beitrag zum Funktionswert leisten. Die ursprüngliche Funktion lässt sich deshalb auch dann mit guter Genauigkeit nähern, wenn man anstatt bis Unendlich nur bis zu einem Index k aufsummiert. Dieser Index k ist dabei ein Glättungsfaktor. Je höher k, desto stärker werden Kurven in den Normierungsdaten mitmodelliert. Um keine Überanpassung zu erhalten, sollte k nicht höher als 5 gewählt werden. In der Regel wird bereits k = 4 zu einer sehr guten Anpassung führen. Je nach Altersverlauf kann es auch vorteilhaft sein, für s etwas höhere Potenzen zu wählen als für t (z. B. s = 5 und t = 3).
Man erhält in der Folge ein endliches Taylorpolynom, welches noch weiter vereinfacht werden kann. Die Fakultäten von s und t sowie die partiellen Ableitungen der Funktion nach l und a an der Stelle P(l0, a0) stellen ebenso wie l0 und a0 einfach Konstanten dar. Eine Ausmultiplikation der Klammern führt deshalb auf das wesentlich vereinfachte Polynom:
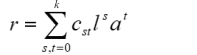
Die Konstanten cst dieses Polynoms können mithilfe multipler Regressionsverfahren aus den manifesten Testdaten geschätzt werden, um eine Hyperfläche anzupassen:
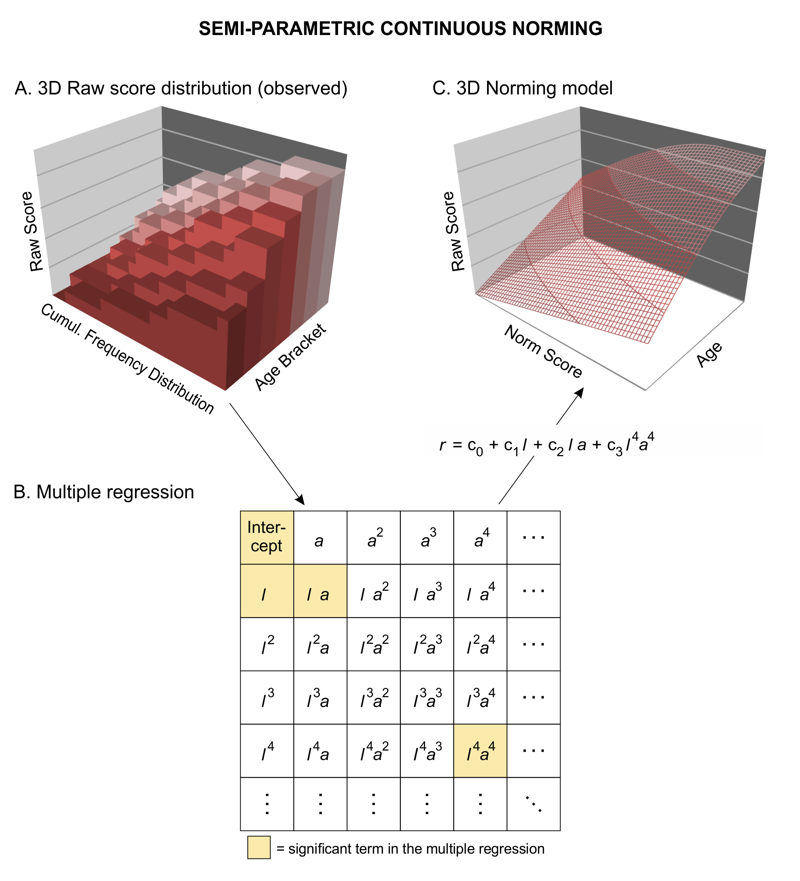
 |
zurück zur verteilungsfreien Modellierung |