cNORM - Verteilungsfreie Modellierung

cNORM - Verteilungsfreie Modellierung

Inhalt

Berechnung der manifesten Normen und Modellierung
Modellselektion
Kreuzvalidierung
Normtabellen erzeugen
Weitere nützliche Funktionen

Berechnung der manifesten Normen und Modellierung

Wie aus der mathematischen Herleitung ersichtlich, basiert die verteilungsfreie Modellierung bei cNORM darauf, dass die Rohwerte als Potenzfunktion der Personlokation l und der explanatorischen Variablen a geschätzt werden. Hierfür sind mehrere Schritte notwendig, die intern aber von einer einzigen Funktion, nämlich der 'cnorm()'-Funktion ausgeführt werden können.

Als erstes schätzt die 'cnorm()'-Funktion vorläufige Werte für die Personenlokation. Dafür werden die Testergebnisse innerhalb jeder Gruppe in eine Rangreihe gebracht. Alternativ kann auch ein gleitendes Fenster zusammen mit der kontinuierlichen explanatorischen Variablen verwendet werden. Hierfür muss die Breite des gleitenden Fensters (Funktionsparameter 'width') angegeben werden. Der Rang wird anschließend mittels Normalrangtransformation in Normwerte umgewandelt. Diese Normwerte dienen als Schätzer für die Personenlokation. Die Personenlokationen können auch unter Einbeziehung von Gewichten berechnet werden, um Verletzungen der Repräsentativität zu kompensieren (siehe Gewichtung).

Der zweite interne Schritt ist die Berechnung von Potenzen für l und a. Die Potenzen werden bis zu einem bestimmten Exponenten 'k' berechnet. Falls für a ein anderer Exponent als für l verwendet werden soll (siehe auch mathematische Herleitung), kann hierfür der Parameter 't' spezifiziert werden. Wenn weder k noch t spezifiziert werden, verwendet die 'cNORM()'-Funktion die Werte k = 5 und t = 3, die sich in der Praxis bewährt haben. Alle Potenzen werden außerdem kreuzweise miteinander multipliziert, um in der anschließenden Regression die Interaktionen von l und a erfassen zu können. Im endgültigen Objekt, das von der 'cnorm()'-Funktion zurückgegeben wird, werden die vorverarbeiteten Daten einschließlich der manifesten Normwerte und aller Potenzen und Interaktionen von l und a in 'model$data' gespeichert.

Im dritten internen Schritt ermittelt 'cnorm' ein Regressionsmodell. Dem Prinzip der Parsimonie folgend sollten dabei am besten solche Modelle ausgewählt werden, die mit möglichst wenigen Prädiktoren eine möglichst hohe Varianzaufklärung erzielen. Die 'cnorm()'-Funktion greift bei der Regression auf die 'regsubset()'-Funktion aus dem 'leaps' package zurück. Dabei sind prinzipiell zwei verschiedene Modellauswahlstrategien möglich: Entweder man gibt vor, wie hoch der Anteil aufgeklärter Varianz (R_adjusted²) mindestens sein soll. Dann wird diejenige Regressionsfunktion ausgewählt, die diese Anforderung mit der geringsten Anzahl an Prädiktoren erreicht. Oder man spezifiziert eine feste Anzahl an Prädiktoren. Dann wird dasjenige Modell ausgewählt, welches mit dieser Zahl an Prädiktoren die höchste Varianzaufklärung erreicht. Leider ist vorab in der Regel nicht bekannt, mit welcher Anzahl an Prädiktoren die Daten optimal angepasst werden können. Wie man diesbezüglich das bestmögliche Modell findet, erläutern wir weiter unten im Abschnitt Modellselektion.

Zum Einstieg möchten wir jedoch erst einmal die grundsätzliche Funktionalität von cNORM anhand eines einfachen Modellierungsbeispiels erläutern. Wir verwenden hierfür den mitgelieferten 'elfe'-Datensatz und beginnen zunächst mit der Standardeinstellung. Diese Einstellung liefert seit der cNORM-Version 3.3.0 das Modell mit der höchsten Varianzaufklärung, bei dem gleichzeitig keine Inkonsistenzen auftreten. (Was wir unter 'Inkonsistenz' verstehen, wird ebenfalls im Abschnitt Modellselektion näher erläutert.)

# Modelliert die Variable 'raw' in Abhängigkeit von der diskreten 'group'-Variable

model <- cnorm(raw = elfe$raw, group = elfe$group)

Die Funktion gibt die folgenden Ergebnisse zurück:

Final solution: 10 terms (highest consistent model)
R-Square Adj. = 0.992668
Final regression model: raw ~ L2 + A3 + L1A1 + L1A2 + L1A3 + L2A1 + L2A2 + L3A1 + L4A3 + L5A3
Regression function: raw ~ 9.364037344 + (-0.005926967039*L2) + (-0.3671738299*A3) + (-0.8979475089*L1A1) + (0.2831824479*L1A2) + (-0.002261103924*L1A3) + (0.0227853959*L2A1) + (-0.005173442779*L2A2) + (-6.018603629e-05*L3A1) + (6.496853126e-08*L4A3) + (-3.964545827e-10*L5A3)
Raw Score RMSE = 0.60987

Use 'printSubset(model)' to get detailed information on the different solutions, 'plotPercentiles(model) to display percentile plot, plotSubset(model)' to inspect model fit.

Das Modell klärt mehr als 99.2 % der Datenvarianz auf, benötigt dafür aber auch die relativ hohe Anzahl von 10 Prädiktoren (plus Intercept). In der Zeile 'Final regression model' wird berichtet, welche Potenzen und Interaktionen bei der Regression einbezogen wurden. L2 steht dabei beispielsweise für die zweite Potenz von l, A3 für die dritte Potenz von a usw.. Die Lokation l wird dabei standardmäßig in T-Werten (M = 50, SD = 10) ausgegeben. Über den Parameter 'scale' lassen sich jedoch auch IQ-Werte, z-Werte, Perzentile oder auch beliebige Vektoren aus Mittelwert und Standardabweichung wählen, z. B. c(10, 3) für Wechsler-Skalenwerte. Nachfolgend wird die komplette Regressionsformel inklusive Koeffizienten zurückgegeben.

Das zurückgegebene Objekt 'model' enthält sowohl die Daten (model$data) als auch das Regressionsmodell (model$model). Alle Informationen über die Modellselektion können unter 'model$model$subsets' abgerufen werden. Der Prozess der Variablenselektion wird Schritt für Schritt in 'outmat' und 'which' aufgelistet. Dort findet man R², R_adjusted², Mallow's C_p und BIC. Die Regressionskoeffizienten für das selektierte Modell ('model$model$coefficients') sind ebenso verfügbar wie die angepassten Werte ('model$model$fitted.values') und alle weiteren Informationen. Eine Tabelle mit den entsprechenden Informationen kann mithilfe des folgenden Codes gedruckt werden:

print(model)

Mathematisch betrachtet stellt die Regressionsfunktion eine sogenannte Hyperfläche im dreidimensionalen Raum dar. Diese Fläche modelliert die manifesten Daten bei ausreichend hohem R² (z. B. R² > .99) in der Regel über weite Bereiche der Normierungsstichprobe sehr gut. Ein Taylorpolynom, wie es hier verwendet wird, besitzt jedoch normalerweise einen endlichen Konvergenzradius. Für die Praxis bedeutet dies, dass es bisweilen Alters- oder Leistungsbereiche geben kann, für welche die Regressionsfunktion keine plausiblen Werte mehr liefert, also z. B. Stellen, an denen das Modell unerwartet stark von den manifesten Daten abweicht. Solche unplausiblen Modellverläufe erkennt man in der Regel am besten, indem man manifeste und modellierte Daten einander grafisch gegenüberstellt. cNORM stellt hierfür unter anderem Perzentildiagramme zur Verfügung. Diese Diagramme können mit folgendem Code erzeugt werden:

# Stellt die modellierten und manifesten Perzentile dar
plot(model, "percentiles")

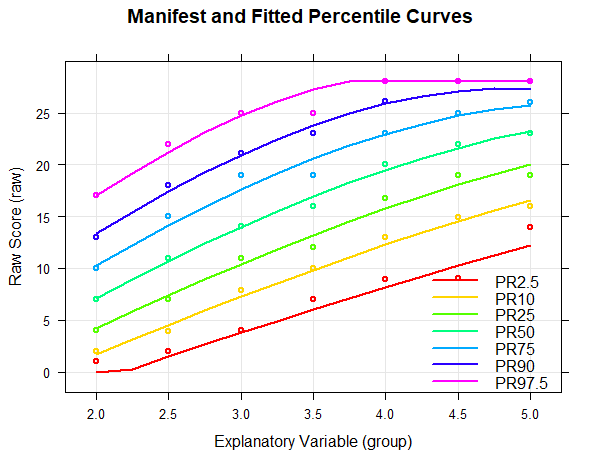
Die manifesten Daten werden im Diagramm als Punkte, die modellierten Perzentile als Linien dargestellt. Der Rohwertebereich wird automatisch basierend auf den Werten aus dem ursprünglichen Datensatz ermittelt. Er kann mittels der Parameter 'minRaw' und 'maxRaw'aber auch explizit angegeben werden.

Wie aus dem obigen Diagramm ersichtlich wird, verlaufen die Perzentile des Normierungsmodells über alle Stufen der explanatorischen Variable hinweg relativ glatt und stimmen gut mit den manifesten Daten überein. Kleine Schwankungen zwischen den einzelnen Gruppen werden eliminiert. Das oberste Perzentilband (PR = 97.5) verläuft zwar ab der vierten Klassenstufe nur noch horizontal. Dies stellt allerdings keine Limitation des Modells, sondern einen Deckeneffekt des Tests dar, da ab hier der maximale Rohwert von 28 erreicht wird. Modellgrenzen treten also nicht nur deshalb auf, weil die Methode nicht perfekt ist, sondern auch, weil die zugrundegelegten Testverfahren nur einen eingeschränkten Messbereich besitzen. Anders ausgedrückt zeigen sich die Grenzen der Modellierbarkeit oft an denjenigen Stellen, an denen der Test zu starke Boden- oder Deckeneffekte besitzt oder an denen die Normierungsstichprobe zu stark ausgedünnt ist. Normalerweise erreicht man die Grenzen der Modellierbarkeit erst an den Rändern des Alters- oder Leistungsbereiches der Normierungsstichprobe oder sogar erst darüber hinaus. Achten Sie deshalb bei der Überprüfung der Perzentillinien vor allem auf die Verläufe des Modells an den Rändern.

Modellselektion

Zwar deutet das Perzentildiagramm auf eine gute Modellpassung hin. Allerdings ist die Anzahl an Prädiktoren mit 10 relativ hoch. Dies birgt die Gefahr, dass es eventuell zu einer Überanpassung der Daten kam. Das deutlichste Zeichen für eine Überanpassung sind normalerweise wellige (und deshalb kontraintuitive) Altersverläufe. Deshalb spricht in diesem Fall nicht allzuviel dafür, dass es sich hierbei tatsächlich um eine relevante Überanpassung handelt. Außerdem kann ein zu starker Fokus auf Sparsamkeit dazu führen, dass die Passung in extremen Leistungsbereichen nicht hoch genug ausfällt. Im Prinzip wäre das vorgeschlagene Modell mit 10 Prädiktoren deshalb durchaus geeignet. Dennoch wollen wir im folgenden die Methoden zeigen, die das cNORM-Package bereit hält, um ggf. noch sparsamere Modelle zu finden.

Als erstes ist es sinnvoll, eine visuelle Inspektion mittels Perzentildiagrammen vorzunehmen. cNORM bietet hierfür eine Funktion an, mit der Perzentilplots mit einer aufsteigenden Anzahl von Prädiktoren als Serie erzeugt werden können.

# Erzeugt eine Serie an Perzentilplots mit aufsteigender Anzahl von Prädiktoren
plotPercentileSeries(model, start = 1, end = 15)

Im vorliegenden Fall wurde eine Serie von Perzentilplots erzeugt, die Modelle von 1 bis 15 Prädiktoren abbildet. An dieser Serie kann man erkennen, dass sich ab 12 Prädiktoren die Perzentillinien in den hohen Klassenstufen kreuzen. Dies bedeutet, dass mit ein und demselben Rohwert zwei verschiedene Normwerte verknüpft wären. Die Abbildung von latenten Personenvariablen auf Rohwerte wäre an dieser Stelle also nicht mehr eineindeutig (=bijektiv) und es wäre demzufolge auch nicht möglich, anhand des Testwertes zwischen diesen Ausprägungen der latenten Variable zu unterscheiden. Ein solcher Befunde stellt eine Modellinkonsistenz dar.

Es kann verschiedene Gründe dafür geben, warum sich Perzentillinien kreuzen.

Der Test weist Boden- oder Deckeneffekte auf. An den Stellen, an denen der minimale oder maximale Rohwert erstmals erreicht wird, schneidet cNORM die Normwerte normalerweise selbstständig ab. In ungünstigen Fällen kann es trotzdem zu überschneidenden Perzentillinien kommen.
Es wurden zu viele Prädiktoren verwendet. Überprüfen Sie, ob Sie mit weniger Prädiktoren ein konsistentes Modell erhalten.
Der Potenzparameter 't' für die explanatorische Variable a wurde zu hoch gewählt. Die meisten Altersverläufe lassen sich mit t = 3 gut abbilden. Falls nur drei Altersgruppen vorliegen, sollte t höchstens auf 2, bei nur zwei Altersgruppen auf 1 gesetzt werden. Höhere Werte sind in diesem Fällen mathematisch nicht sinnvoll.
Das Regressionsmodell wird auf Alters- oder Leistungsbereiche ausgedehnt, die in der Normierungsstichprobe nicht oder selten vorkamen. Zwar ist es rein mathematisch möglich, Alters- und Leistungsbereich abzudecken, die nicht in der Normierungsstichprobe vorkamen. Allerdings sollte eine solche Extrapolation ohne empirische Grundlage mit äußerster Vorsicht und Zurückhaltung vorgenommen werden.

Wenn der Potenzparameter 't' für die explanatorische Variable a zu hoch gewählt wurde, können neben kreuzenden Perzentillinien auch sehr wellige Altersverläufe auftreten. Zum Vergleich finden Sie im Folgenden die Serie an Perzentilplots, die man erhalten würde, wenn man k = 5 und t = 4 wählen würde.

Bei 14 Prädiktoren sieht man deutliche Wellen im unteren Perzentilband, aber auch schon ab 7 Prädiktoren ist der Altersverlauf der Perzentilbänder nicht mehr so gleichmäßig, wie man dies eigentlich wünschen würde. Achten Sie also beim Modellieren darauf, ob die Altersverläufe in allen Bereichen Ihren Erwartungen entsprechen und verändern Sie ggf. den Potenzparameter t und die Anzahl an Prädiktoren so lange, bis ein Modell mit den gewünschten Eigenschaften gefunden wird.

Kehren wir also wieder zu unsere Modellserie mit k = 5 und t = 3 zurück, die offensichtlich bessere Ergebnisse liefert als k = 5 und t = 4. Unser Ziel bestand ja darin, ggf. noch Modelle zu finden, die mit weniger als 10 Prädiktoren ausreichend gute Modellierungsergebnisse liefern. Zu diesem Zweck können Sie sich auch anschauen, wie sich die Hinzunahme von Prädiktoren auf R_adjusted² auswirkt. Verwenden Sie hierfür den folgenden Befehl:

plot(model, "subset", type = 0)

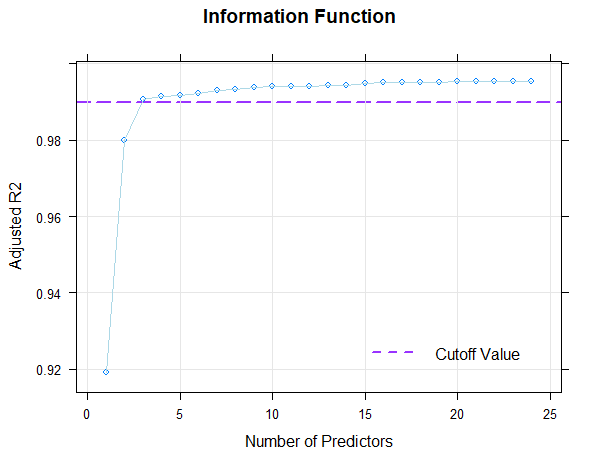
Wenn in der Funktion 'plot()' type = 1 anstatt type = 0 gesetzt wird, dann wird Mallow's C_p in logarithmierter Form ausgegeben. Mit type = 2 wird der BIC (type = 2) über R_adjusted² aufgetragen.

Dass man eine relativ gut modellierbare Skala vorliegen hat, erkennt man daran, dass es möglich ist, konsistente Modelle zu finden, die mehr als 99 % der Datenvarianz erklären. Im vorliegenden Fall wird dieser Wert bereits mit drei Prädiktoren erreicht (R_adjusted² = .991). Im Prinzip liegen hier also eine ganze Reihe an sparsameren Modellen vor, die zur Auswahl in Frage kämen. Mit 8 Prädiktoren werden 99.3 % der Datenvarianz durch das Modell erklärt, also nur 0.2 % mehr als mit drei Prädiktoren. Allerdings führen selbst Erhöhungen im Promillebereich in extremen Leistungsbereichen bisweilen zu bedeutsamen Verbesserungen des Normierungsmodells. Über 8 Prädiktoren hinaus führt eine weitere Hinzunahme von Prädiktoren hingegen nicht einmal mehr zu Veränderungen im Promillebereich. Modelle zwischen 3 und 8 Prädiktoren scheinen also prinzipiell geeignet zu sein. Welches Modell davon am Ende ausgewählt werden sollte, entscheiden wir mittels der folgenden Kreuzvalidierung.

Kreuzvalidierung

Wie bereits weiter oben beschrieben, besteht das Ziel des Modellierungsprozesses nicht unbedingt darin, maximale Varianzaufklärung zu erreichen. Eine zu enge Anpassung des Modells an die Trainingsdaten stellt nämlich mit hoher Wahrscheinlichkeit eine Überanpassung an die (fehlerbehaftete) Stichprobe dar. Stattdessen sollen die Modelle die (in der Regel unbekannte) Verteilung in der Referenzpopulation möglichst gut vorhersagen. Um abzuschätzen, wie gut dies gelingt, kann zusätzlich eine Kreuzvalidierung durchgeführt werden. Dabei werden wiederholt 80 Prozent der Daten als Trainingsdaten gezogen und an den verbleibenden 20 Prozent validiert. Die Trainingsdaten werden nach Normgruppe geschichtet, aber innerhalb jeder Normgruppe randomisiert gezogen. Wie bei den Perzentilserien werden auch bei der Kreuzvalidierung Modelle mit zunehmender Anzahl von Termen (d. h. Prädiktoren) berechnet. Für jede Anzahl von Termen werden für die Trainingsdaten, die Validierungsdaten und den kompletten Datensatz jeweils der RMSE (bezogen auf Rohwerte oder Normwerte) und R² (bezogen auf Normwerte) berechnet. Zusätzlich kann der 'Crossfit' als Verhältnis von R² in Training und Validierung berechnet werden.

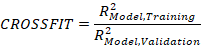
Der Crossfit liegt in aller Regel höher als 1, da ein Modell auf Trainingsdaten immer besser passt als auf neue Daten. Je höher er liegt, desto stärker deutet dies allerdings auf eine Überanpassung der Daten hin. Der Crossfit sollte also möglichst nahe an 1 liegen, da das Modell auf die Validierungsdaten dann zumindest ähnlich gut passt wie auf die Trainingsdaten. Gut ist ein solches Modell allerdings nur dann, wenn gleichzeitig der RMSE in den Validierungsdaten möglichst niedrig (bzw. R² möglichst hoch) ausfällt. Außerdem sollte auch der Standardfehler der Normwerte in den Validierungsdaten möglichst niedrig ausfallen, da das Modell dann eine stabile Passung besitzt.

Das folgende Beispiel berechnet eine Kreuzvalidierung auf Basis des elfe-Datensatzes mit 30 Wiederholungen und einer Anzahl von 3 bis 8 Termen in der Regressionsfunktion:

model <- cnorm(raw = elfe$raw, group = elfe$group)
cnorm.cv(model$data, repetitions = 30, min = 3, max = 8)

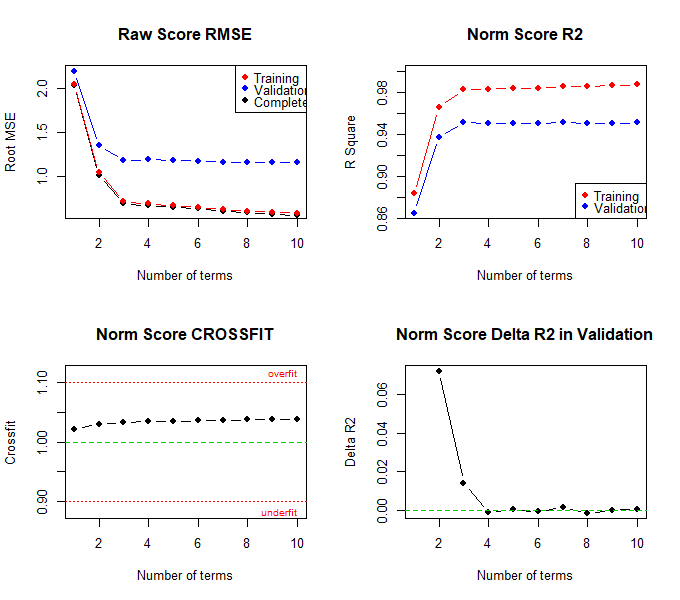
Die Ergebnisse deuten darauf hin, dass ein Modell mit 4 Termen vermutlich das beste Modell darstellt. Der RMSE der Normwerte liegt hier in den Validierungsdaten am niedrigsten, R² am höchsten. Der Crossfit fällt zwar nicht am niedrigsten aus, liegt aber näher an 1 als beim Modell mit 3 Prädiktoren. Außerdem liegt auch der Standardfehler der Normwerte niedriger als im Modell mit 3 Prädiktoren. Auch das Perzentildiagramm sah ja bei 4 Prädiktoren bereits sehr gut aus. Das Modell mit 4 Prädiktoren sollte deshalb ausgewählt werden. Um dieses Modell zu ermitteln, muss eine Neuberechnung durchgeführt werden. Diesmal spezifizieren wir bei dieser Berechnung die Anzahl der Prädiktoren:

# Berechnet das Modell mit 4 Prädiktoren

model <- cnorm(raw = elfe$raw, group = elfe$group, terms = 4)

Das finale Modell sieht folgendermaßen aus:

User specified solution: 4 terms
R-Square Adj. = 0.991412
Final regression model: raw ~ A3 + L1A2 + L2A1 + L2A2
Regression function: raw ~ -8.562056855 + (-0.08913080094*A3) + (0.05168132497*L1A2) + (0.003164634892*L2A1) + (-0.0009790480969*L2A2)
Raw Score RMSE = 0.66148

Zwar sind im Perzentildiagramm des Modells mit 4 Prädiktoren keine sich kreuzenden Perzentillinien erkennbar. Jedoch liegt das niedrigste Perzentil standardmäßig nur bei PR 2.5 und das höchste Perzentil bei PR 97.5. Theoretisch könnten also kreuzende Perzentillinien in extremeren Leistungsbereichen vorkommen. Falls Normwerte ausgegeben werden sollen, die über das hinausgehen, was im Perzentildiagramm dargestellt wurde, dann sollten die Grenzen der Modellgültigkeit also noch genauer spezifiziert werden. Dies kann z. B. grafisch vorgenommen werden, und zwar indem im Perzentildiagramm ein Vektor mit Perzentilen spezifiziert wird, der aufgetragen werden soll.

# Perzentildiagramm mit den Perzentilen PR 1, 5, 10, 90, 95 und 99

plotPercentiles(model, percentiles = c(0.01, 0.05, 0.1, 0.9, .95, 0.99))

Noch einfacher können sich überschneidende Perzentillinien mit der Funktion "checkConsistency" ermittelt werden. Beachten Sie jedoch, dass Inkonsistenzen umso wahrscheinlicher gefunden werden, je extremer die überprüften Lokationen sind. Wir beschränken uns deshalb auf den für diese Testskala sinnvollen T-Wertebereich von 25 bis 75:

# Suche nach sich überschneidenden Perzentilen
checkConsistency(model, minNorm = 25, maxNorm = 75)

Die Funktion liefert glücklicherweise zurück, dass innerhalb dieses Bereichs keine Inkonsistenzen gefunden wurden. Das ausgewählte Modell ist also mindestens zwischen den T-Werten 25 und 75 konsistent. Sollte sich ein Modell nach Prüfung der Konsistenz doch als suboptimal herausstellen, empfiehlt es sich, die Anzahl an Prädiktoren zu verändern oder gegebenenfalls auch k oder t anders zu wählen. Normtabellen und Normwerte sollten selbstverständlich nur innerhalb des Gültigkeitsbereichs des Regressionsmodells ausgegeben werden. Außerdem sollte sich der Normwertbereich auch an der Größe der Normierungsstichprobe orientieren. So liegt beispielsweise die Wahrscheinlichkeit, dass sich in einer Stichprobe der Größe N = 500 keine einzige Person mit einem T-Wert von 20 oder niedriger befindet, bei über 50 %. T-Werte von 20 oder niedriger (bzw. 80 oder höher) sollten für solche Stichprobengrößen also nicht tabelliert werden, da die Regressionsmodelle an solchen Stellen mit hoher Unsicherheit behaftet sind.

Normtabellen erzeugen

Über die reinen Modellierungsfunktionen hinaus enthält cNORM auch Funktionen, die der Generierung von Normtabellen und dem Abruf von Normwerten zu spezifischen Rohwerten (und umgekehrt) dienen:

predictNorm

Die Funktion 'predictNorm' gibt zu einem bestimmten Rohwert (z. B. raw = 15) und einem spezifischen Alter (z. B. a = 4.7) den zugehörigen Normwert zurück. Die Normwerte müssen dabei auf einen Minimal- und Maximalwert begrenzt werden, um die Grenzen der Modellvalidität zu berücksichtigen.

predictNorm(15, 4.7, model, minNorm = 25, maxNorm = 75)

predictRaw

Die Funktion 'predictRaw' gibt zu einem bestimmten Normwert (z. B. T = 55) und einer bestimmten Altersstufe (z. B. a = 4.5) den modellierten Rohwert zurück.

predictRaw(55, 4.5, model, minRaw = 0, maxRaw = 28)

normTable

Die Funktion 'normTable' gibt für ein bestimmtes Alter (z. B. a = 3) zu einer vorspezifizierten Reihe an Normwerten die zugehörigen Rohwerte aus. Der Parameter 'step' spezifiziert dabei den Abstand zwischen zwei Normwerten.

normTable(3, model, minRaw = 0, maxRaw = 28, minNorm=30.5, maxNorm=69.5, step = 1)

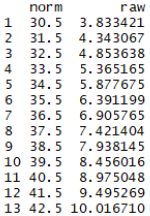
Diese Funktion ist vor allem dann sinnvoll, wenn Skalen einen großen Rohwertebereich haben und deshalb zu einem (gerundeten) Normwert mehrere Rohwerte gehören. Zu einem tabellierten Normwert T = 40 müssten dann beispielsweise alle ganzzahligen Rohwerte aufgeführt werden, die Normwerten zwischen 39.5 und 40.5 zugeordnet sind. Im vorliegenden Fall gehört zu T = 39.5 der Rohwert 8.47 und zu T = 40.5 der Rohwert 8.99. Einem im Testhandbuch tabellierten Normwert von 40 wäre damit kein einziger (ganzahliger) Rohwert zuzuordnen. Außerdem ist die Funktion 'normTable()' auch dann sinnvoll, wenn in einer einzigen Tabellen des Testhandbuchs Normwerte zu verschiedenen Untertests tabelliert werden sollen.

rawTable

Die Funktion 'rawTable' ist vergleichbar mit 'normTable', kehrt aber die Zuordnung um: Einer vorspezifizierten Reihe an Rohwerten werden für ein bestimmtes Alter die Normwerte zugeordnet. Hierfür ist eine Umkehrung der Regressionsfunktion erforderlich, die numerisch ermittelt wird. Wenn in der 'rawTable'-Funktion zusätzlich noch ein Konfidenz- und ein Reliabilitätskoeffizient spezifiziert werden, dann wird die Tabelle mit Konfidenzintervallen ausgegeben.

rawTable(3.5, model, minRaw = 0, maxRaw = 28, minNorm = 25, maxNorm = 75, step = 1, CI = .95, reliability = .89)

# Mehrere Tabellen auf einmal generieren

table <- rawTable(c(2.5, 3.5, 4.5), model, minRaw = 0, maxRaw = 28)

Eine solche Tabelle benötigt man, wenn man zu allen vorkommenden Rohwerten das genaue Perzentil oder den genauen Normwert bestimmen möchte.

Weitere nützliche Funktionen

Plot der Rohwerte

In den folgenden Diagrammen werden die manifesten und die modellierten Rohwerte einander für jede (Alters-)gruppe getrennt gegenübergestellt. Wird die Angabe zu 'group' auf 'FALSE' gesetzt, dann werden die Werte über den gesamten Bereich der explanatorischen Variable (d. h. ohne Gruppenunterscheidung) geplottet.

plot(model, "raw", group = TRUE)

Die Anpassung ist dann besonders gut, wenn alle Punkte möglichst nah an der Winkelhalbierenden liegen. Hierbei muss allerdings beachtet werden, dass Abweichungen im extremen oberen, vor allem aber im extremen unteren Leistungsbereich oft auch deshalb zustande kommen, weil die manifesten Daten in diesen Bereichen ebenfalls mit großen Messunsicherheiten verknüpft sind.

Plot der Normwerte

Die Funktion entspricht der Funktion plot("raw"), nur dass hier die manifesten und projizierten Normwerte gegeneinander geplottet werden. Bitte geben Sie zudem die Grenzen des Normwertbereichs an. Im konkreten Beispiel sind dies T-Werte von 25 bis 75. Die Werte decken also den Bereich von -2.5 bis +2.5 Standardabweichungen um den Mittelwert ab.

plot(model, "norm", group = TRUE, minNorm = 25, maxNorm = 75)

Dichtefunktionen

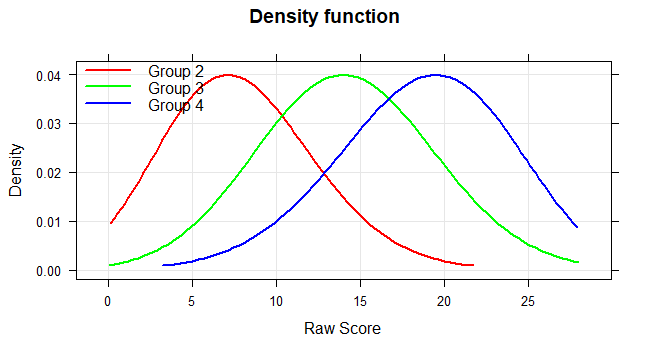
Die 'plot("density")'-Funktion stellt die vom Modell geschätzte Wahrscheinlichkeitsdichte für die Rohwerte dar. Die Methode kann genutzt werden, um Abweichung der Testergebnisse von der Normalverteilung besser sichtbar zu machen.

plot(model, "density", group = c (2, 3, 4))

Analytische Überprüfung der Regressionsfunktion

Zu guter Letzt wollen wir die mathematisch versierten Anwender an dieser Stelle außerdem auch auf die Möglichkeit hinweisen, die Regressionsfunktion analytisch noch weiter zu überprüfen. Da es sich bei der Regressionsgleichung ja um ein in mathematischer Hinsicht sehr leicht zu handhabendes Polynom n-ten Grades handelt, kann dieses nämlich einer herkömmlichen Kurvendiskussion unterzogen werden. Damit lässt sich beispielsweise sehr leicht feststellen, an welchen Stellen Extrema, Wendepunkte, Sattelpunkte usw. vorkommen.

In diesem Zusammenhang steht auch die 'plot("derivative")'-Funktion zur Verfügung. Mit dieser Funktion lässt sich die erste partielle Ableitung der Regressionsfunktion nach der Personenlokation grafisch darstellen. So lässt sich beispielsweise leicht überprüfen, an welchen Stellen diese Ableitung einen Nulldurchgang hat. An diesen Stellen kommt die Modellgültigkeit normalerweise an ihre Grenzen.