Site menu:

cNORM - Beispiele

Inhalt

1. Modellierung eines Wortschatztests von 2 bis 17 Jahren
2. Biometrie: Modellierung des BMI von 2 bis 25 Jahren
3. Modellierung von Reaktions- und Bearbeitungszeiten
4. Abschlussbemerkung

Im Folgenden möchten wir Ihnen drei weitere Beispiele zur Verwendung von cNORM vorstellen. Die ersten beiden können Sie mit den bereits im Package enthaltenen Daten nachvollziehen. Installieren Sie hierfür zunächst cNORM und aktivieren Sie die cNORM-Bibliothek.

1. Modellierung eines Wortschatztests von 2 bis 17 Jahren

Anhand des Datensatzes, der bei der folgenden Modellierung zum Einsatz kommt, haben wir bereits die parametrische Normierung mittels der Beta-Binomialverteilung demonstriert. Es handelt sich dabei um eine unselektierte Stichprobe aus der deutschlandweiten Erhebung eines Wortschatztests (Beispieldatensatz 'ppvt'). Dieser Datensatz enthält im Gegensatz zum 'elfe'-Datensatz keine Gruppierungsvariable, sondern eine kontinuierliche Altersvariable, die in diesem Fall als explanatorische Variable herangezogen werden soll. Für die Ermittlung der Perzentile verwenden wir diesmal ein 'Sliding Window'.

# Ermittlung der manifesten Perzentile und Normwerte mittels 'Sliding Window'
# Die Größe des Fensters beträgt hier 1.0 Jahre.

model.ppvt <- cnorm(raw=ppvt$raw, age=ppvt$age, width=1)

Das zurückgelieferte Modell klärt 99.23 % der Datenvarianz auf. Die Daten lassen sich also hervorragend modellieren. Wenn weder R_adjust² noch die Anzahl an Termen spezifiziert wird, dann liefert uns die cnorm()-Funktion allerdings zunächst das Modell mit der höchsten Varianzaufklärung zurück, bei dem keine größeren Inkonsistenzen gefunden werden. Das zurückgelieferte Modell hat deshalb die sehr hohe Anzahl von 19 Prädiktoren. Es sollte also nach einem sparsameren Modell gesucht werden. Hierfür schauen wir uns zunächst an, wie sich die Aufnahme von Prädiktoren auf die Varianzaufklärung auswirkt.

# Darstellung von R_adj.² als Funktion der Anzahl an Prädiktoren

plot(model.ppvt, "subset", type=0)

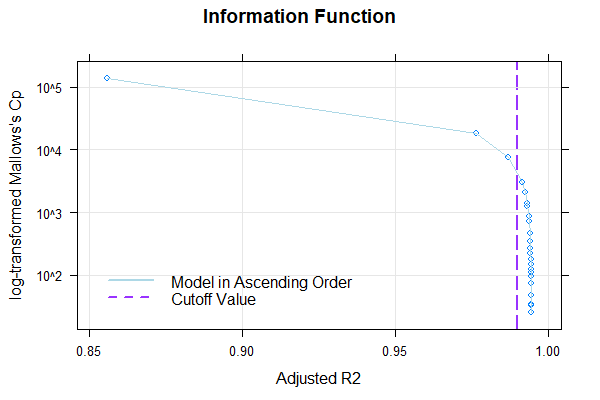
Der Plot zeigt, dass sich R_adj.² ab 6 Prädiktoren nicht mehr wesentlich verändert. Um die Modellpassungen auch mittels der Perzentildiagramme zur Überprüfen, erzeugen wir als nächstes eine Serie an Perzentilplots mit 3 bis 15 Prädiktoren.

# Erzeugt eine Serie an Perzentilplots mit aufsteigender Anzahl von Prädiktoren

plotPercentileSeries(model.ppvt, start = 3, end = 15)

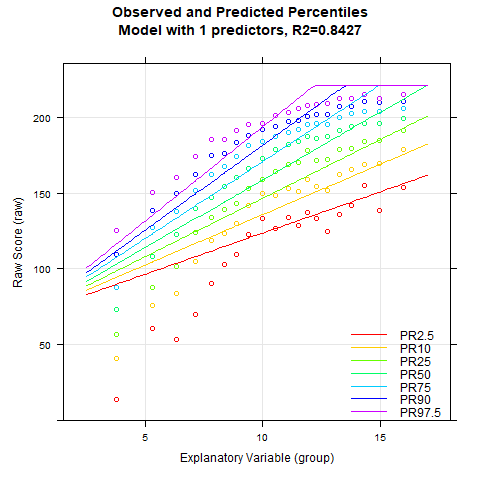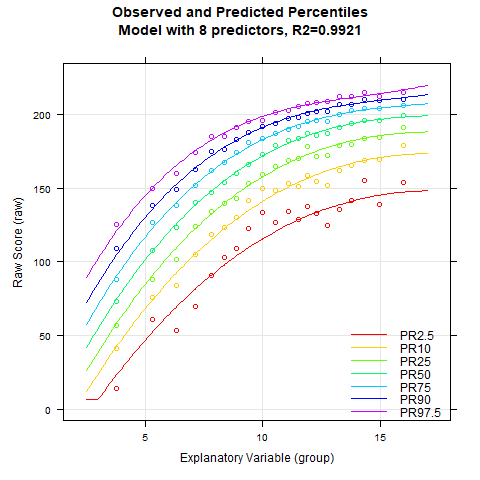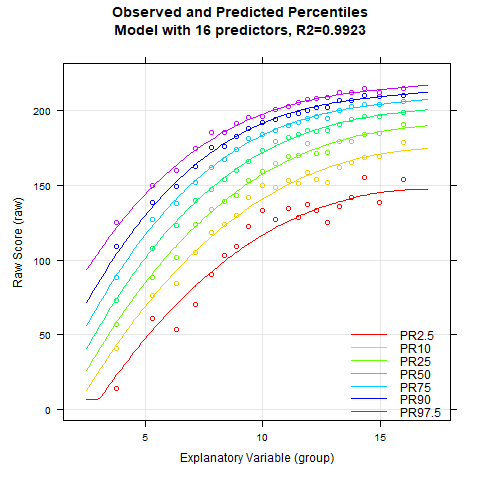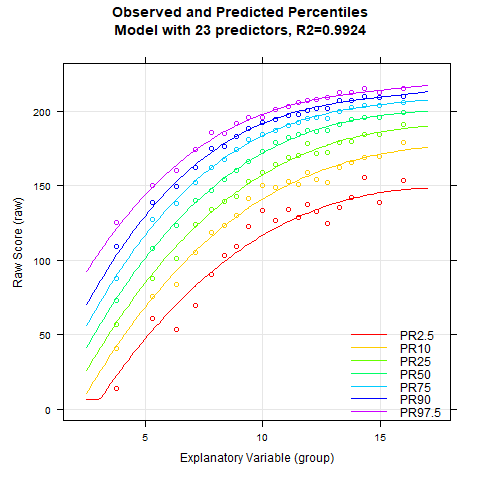
Zwar sieht der Perzentilplot tatsächlich bereits mit 5 Prädiktoren schön glatt aus. Bei genauerer Inspektion kann man allerdings erkennen, dass sich bei dieser niedrigen Anzahl an Prädiktoren die Perzentillinien bei hohen Altersstufen im hohen Leistungsbereich nach oben weg biegen. Dies ist ein Effekt, der sicherlich nicht den realen Gegebenheiten entspricht. Vielmehr würde man erwarten, dass alle Perzentillinien in den höheren Altersbereichen zunehmend flach verlaufen. Bei dem Modell mit 9 Prädiktoren ist dieser unerwünschte Effekt kaum noch sichtbar, ab 12 Prädiktoren verschwindet er ganz. Zur Kontrolle rechnen wird deshalb auch noch eine Kreuzvalidierung. Wegen des 'sliding windows" dauert dies eine Weile. Die Anzahl der Wiederholungen wird deshalb "nur" auf 10 Wiederholungen gesetzt.

cnorm.cv(model.ppvt$data, repetitions = 10, min = 3, max = 12)

In der Kreuzvalidierung schneiden die Modelle mit 9 bzw. mit 12 Prädiktoren nicht besser, aber auch nicht schlechter ab als das Modell mit nur 7 Prädiktoren. Vom visuellen Eindruck her sieht aber tatsächlich das Modell mit 12 Prädiktoren am besten aus. Wir prüfen deshalb die Modelle zuletzt noch auf ihre Konsistenz. Am genauesten geht dies tatsächlich mit der 'plot("derivative")'-Funktion, die wir in diesem Fall auch heranziehen. Diese Funktion stellt die erste partielle Ableitung der Regressionsfunktion nach der Personenlokation dar. Da die Normwerte im vorliegenden Fall umso höher ausfallen müssen, je höher der Rohwert im Test ist, sollte diese partielle Ableitung nie negativ werden. Im Falle eines Boden- oder Deckeneffektes würde sie höchstens 0 betragen dürfen.

Weil wir hier die drei Modelle mit 7, 9 oder 12 Prädiktoren miteinander vergleichen wollen, es hierfür aber keine "Serienfunktion" wie bei 'plotPercentileSeries()' gibt, müssen wir zuerst jeweils die Modelle berechnen und anschließend die 'plot("derivative")'-Funktion darauf anwenden.

# Prüft die Grenzen der Modellvalidität mittels der ersten partiellen
# Ableitung nach der Lokation innerhalb des angegebenen Altersbereichs.
# Die Ableitung sollte keinen Nulldurchgang aufweisen.

model.ppvt7 <- cnorm(raw=ppvt$raw, age=ppvt$age, width=1, terms = 7)
plot(model.ppvt7, "derivative", minAge=2, maxAge=20, minNorm=20, maxNorm=80)

model.ppvt9 <- cnorm(raw=ppvt$raw, age=ppvt$age, width=1, terms = 9)
plot(model.ppvt9, "derivative", minAge=2, maxAge=20, minNorm=20, maxNorm=80)

model.ppvt12 <- cnorm(raw=ppvt$raw, age=ppvt$age, width=1, terms = 12)
plot(model.ppvt12, "derivative", minAge=2, maxAge=20, minNorm=20, maxNorm=80)

Das Ergebnis sieht folgendermaßen aus:

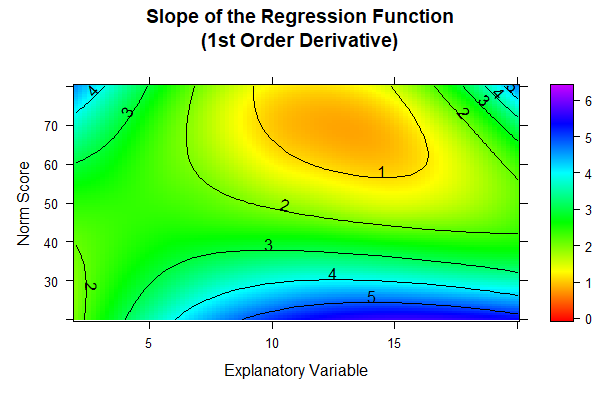
Die Farben der Grafik werden jeweils individuell an den vorhandenen Wertebereich angepasst. Da dieser beim Modell mit 12 Prädiktoren am größten ausfällt, lassen sich die Farben zwischen den drei Abbildungen nicht hundertprozentig miteinander vergleichen. Allerdings ist bei den Modellen mit 7 und 9 Prädiktoren jeweils am oberen Rand des Bildes eines schwarze gestrichelte Linie erkennbar. Diese markiert den Nulldurchgang. Im Alter zwischen etwa 12 und 15 Jahren gibt es also bei diesen Modellen im ganz hohen Leistungsbereich (nahe T-Wert = 80) Inkonsistenzen. Beim Modell mit 12 Prädiktoren ist ein solcher Nulldurchgang nicht vorhanden. Das Modell ist also nicht hinsichtlich der Modellpassung, wohl aber hinsichtlich der Konsistenz besser als die beiden anderen und sollte deshalb ausgewählt werden.

Allerdings sollte an einer solchen Stelle, an der der Test offensichtlich zumindest einen leichten Deckeneffekt aufweist, auch überlegt werden, ob es überhaupt sinnvoll und notwendig ist, den Test bis zu einem T-Wert von 80 zu tabellieren. Auch wenn - wie in diesem Fall - die Stichprobe mit N = 4542 recht groß war, so ist der Normierungsfehler in der Regel bei einer Leistung, die drei Standardabweichungen vom Populationsmittelwert entfernt liegt, trotzdem relativ hoch. Schließlich erwartet man rein statistisch selbst in der gesamten Stichprobe (d. h. über alle Altersstufen hinweg) nur etwa 6 Kinder, die tatsächlich einen T-Wert von 80 oder höher aufweisen. Im Prinzip sind T-Werte von 80 oder höher (und gleichermaßen von 20 oder niedriger) also nicht mehr gut empirisch verankert.

Eine ähnliche Frage stellt sich übrigens, wenn es darum geht, bis zu welchem Alter Normwerte ausgewiesen werden sollen. Tatsächlich enthält der Datensatz keine Person, die über 17 Jahre alt sind. Trotzdem könnte die Regressionsfunktion natürlich theoretisch auch auf Altersbereiche ausgeweitet werden, die gar nicht in der Normierungsstichprobe vorkamen. Bei den Ableitungsdiagrammen haben wir uns den Bereich bis zum Alter von 20 Jahren darstellen lassen. Modellinkonsistenzen in Form von Nulldurchgängen der Ableitung sind bei 12 Prädiktoren auch in diesem hohen Altersbereich nicht erkennbar. Trotzdem möchten wir vor solchen Extrapolationen warnen. Testnormen sollten immer in der Empirie verankert sein. Speziell die Extrapolationen in Altersbereiche, die in der Normierungsstichprobe gar nicht vorkamen, bergen sowohl bei der verteilungsfreien als auch bei der parametrischen Normierung die Gefahr, dass hier nur noch Hausnummern gemessen werden.

Vergleich zwischen verteilungsfreier und parametrischer Normierung

Im Kapitel über parametrische Normierung hatten wir ja bereits gezeigt, dass man den ppvt-Datensatz auch mittels Beta-Binomialverteilung normieren kann. Wir wollen deshalb das Ergebnis der verteilungsfreien Modellierung einmal direkt mit dem Ergebnis der parametrischen Modellierung vergleichen. Wir tun dies grafisch. Dafür haben wir die Perzentilplots der beiden Modelle übereinandergelegt. Im cNORM-Package steht dafür bislang leider keine Funktion zur Verfügung. Die nachfolgende Grafik wurde also mit anderer Software erzeugt.

Im dargestellten Perzentilplot stellen die Punkte die manifesten Daten, die durchgezogenen Linien die verteilungsfreie Normierung und die gestrichelten Linien die parametrische Normierung dar. Innerhalb desjenigen Altersbereichs, der tatsächlich in der Normierungsstichprobe vertreten war (2 Jahre 6 Monate bis 16 Jahre 11 Monate), stimmen beide Modelle in weiten Leistungsbereich sehr gut miteinander überein. Lediglich im stark unterdurchschnittlichen Bereich (PR 2.5) finden sich größere Abweichungen. Allerdings weisen die manifesten Daten im stark unterdurchschnittlichen Leistungsbereich ebenfalls große Unsicherheiten auf, was man daran erkennen kann, dass die roten Punkte keinem glatten, sondern einem sehr gezackten Altersverlauf folgen. Hier scheint also die Messunsicherheit generell sehr hoch zu sein, was sich dann eben auch in den Unsicherheiten bei der Modellierung widerspiegelt. Zumindest scheint die verteilungsfreie Modellierung etwas näher an den manifesten Daten zu liegen, als dies bei der parametrischen Modellierung der Fall ist, wo die PR 2.5-Linie im Schnitt etwas zu hoch zu liegen scheint. Ob durch die verteilungsfreie Modellierung aber tatsächlich auch die Verteilung in der Population besser widergespiegelt wird, hängt letzten Endes dann natürlich davon ab, wie gut die Stichprobe die Population widerspiegelt. Leider ist dies eine Frage, die im vorliegenden Fall nicht endgültig beantwortet werden kann.

Erzeugung von Normtabellen

Zum Schluss wollen wir noch Normtabellen erzeugen, die als Excel-Dateien auf dem Rechner abgespeichert werden sollen. Hier muss zunächst überlegt werden, welcher Bereich für die Normwerte gewählt werden sollte. Wir hatten gerade festgestellt, dass bereits die PR 2.5-Linie mit relativ viel Mess- und Normierungsunsicherheit verknüpft ist. Die Ausgabe noch extremerer Normwerte ist deshalb wenig zielführend. Wir beschränken uns deshalb auf Werte zwischen PR 2.5 und PR 97.5. Dies entspricht in etwa T-Werten zwischen 30 und 70.

Die nächste Frage betrifft die Art der Normtabelle. Da der PPVT 228 Items hat, ist es nicht angebracht, für jeden möglichen Rohwert einen Normwert zu tabellieren. Vielmehr empfiehlt es sich, zu ganzzahligen T-Werten den entsprechenden Rohwertebereich zu tabellieren. Wir wählen deshalb die Funktion 'normTable()'. Dabei sollten wir und klar machen, dass ganzzahlig abgestufte T-Werte in so einer Tabelle in Wirklichkeit T-Wert-Intervalle repräsentieren. Ein T-Wert von 50 repräsentiert z. B. ein T-Wert-Intervall von 49.5 bis 50.5. Zu einem T-Wert von 50 müssen dann alle (ganzzahligen) Rohwerte tabelliert werden, die innerhalb des zugehörigen Intervalls liegen. Bei der Erzeugung der Normtabelle wählen wir deshalb die Intervallgrenzen und nicht die Intervallmitten. So können wir später feststellen, welche Rohwerte jeweils im zugehörigen T-Wert-Intervall vorkommen. An der unteren und oberen Grenze des Bereiches können wir die zugehörigen Rohwerte im Testhandbuch später jeweils mit "≤" und "≥" spezifizieren.

Eine nächste Frage betrifft die Altersabstufung. Ein Vorteil der kontinuierlichen Normierung ist ja gerade derjenige, dass der Genauigkeit hier keine Grenzen gesetzt sind. Auf der anderen Seite sind zwei verschiedene Alterstabellen sinnlos, wenn in den beiden Tabellen die gleichen Zahlenwerte zu finden sind. Die Altersintervalle sollten deshalb so groß gewählt werden, dass Änderungen in der Zuordnung zwischen Rohwerten und Normwerten klein aber erkennbar sind. Im vorliegenden Beispiel wählen wir für 11-jährige Kinder Vierteljahres-Intervalle. Die Altersstufen, die in der Funktion spezifiziert sind, entsprechen jeweils den zugehörigen Intervallmitten.

Außerdem wollen wir die Tabellen noch auf dem Rechner abspeichern, um sie später (z. B. auf Excel) weiterverarbeiten zu können. Hierfür kann z. B. das Package 'openxlsx' verwendet werden, das wir zunächst ggf. noch installieren müssen:

# Installiert das openslxs Package und
# ruft die zugehörige Bibliothek auf

install.packages("openxlsx", dependencies = TRUE)
library(openxlsx)

# Erzeugt die gewünschten Normtabellen und
# schreibt sie ins angegebene Verzeichnis

write.xlsx(normTable(c(11.125,11.375, 11.625, 11.875), model.ppvt12, minNorm=30.5, maxNorm=69.5, step = 1), file = "C:/Users/Documents/cnorm/normTables_ppvt_11.xlsx")

Bitte beachten Sie, dass in den jetzt abgespeicherten Normwerttabellen tatsächlich nur die Norm- und Rohwerte an den Intervallgrenzen als Dezimalzahlen ausgegeben werden. Tabellen, in denen zu jedem ganzzahligen Normwert ein ganzzahliger Rohwertbereich tabelliert ist, müssen aus diesen Tabellen also erst noch durch Auf- und Abrunden der jeweiligen Intervallgrenzen erzeugt werden. Aber das ist ein Stück Arbeit, das Sie sicherlich auch ohne unsere Hilfe schaffen.

2. Biometrie: Modellierung des BMI im Alter von 2 bis 25 Jahren

Nicht nur psychische Personeneigenschaften, sondern auch biometrische Daten lassen sich mittels cNORM modellieren. Dies demonstrieren wir anhand eines Datensatzes des Center of Disease Control (CDC, 2012), der im cNORM Package mitgeliefert wird und Rohdaten über die Entwicklung des Body-Mass-Index enthält. Eine Beschreibung des Datensatzes ist in den Hilfedateien des cNORM-packages verfügbar. Der Body-Mass-Index ist eine kontinuierliche Variable. Sie kann deshalb nicht mit der Beta-Binomialverteilung modelliert werden. Außerdem verläuft die Entwicklung des BMI für Jungen und Mädchen eigentlich unterschiedlich. Wir müssten also zwei verschiedene Kurven modellieren. Der Einfachheit halber demonstrieren wir die Modellierung jedoch anhand des gesamten Datensatzes.

Wie die Ergebnisse für Mädchen und Jungen getrennt aussehen würden, können Sie gerne zur Übung selbst ausprobieren. Übrigens: Zum Erzeugen zweier nach Geschlecht getrennter Datensätze können Sie den folgenden Code verwenden:

# Erzeugt zwei getrennte Datensätze für Jungen und Mädchen

CDC_male <- CDC[CDC$sex==1,]
CDC_female <- CDC[CDC$sex==2,]

Wir machen an dieser Stelle aber mit dem ursprünglichen Datensatz weiter. Da dieser sehr groß ist, wird das Ranking zur Reduzierung des Rechenaufwands über die im Datensatz vorhandene diskrete Gruppierungsvariable vorgenommen. Alle weiteren Modellierungsschritte erfolgen über die kontinuierliche Altersvariable.

# Ermittlung eines Models für die BMI-Variable

model.bmi <- cnorm(raw=CDC$bmi, group=CDC$group)

Wieder liefert uns die cnorm()-Funktion ohne Spezifikation der Anzahl an Termen dasjenige Modell zurück, das maximal viel Datenvarianz erklärt, ohne dabei signifikante Inkonsistenzen aufzuweisen. R_adj² liegt bei 99.33 %, die Anzahl an Prädiktoren beträgt dabei aber sage und schreibe 23. Wir machen uns deshalb auf die Suche nach einem sparsameren Modell. Als erstes schauen wir uns hierfür wieder an, wie die Varianzaufklärung durch die Anzahl an Prädiktoren beeinflusst wird:

# Darstellung von R_adj.² als Funktion der Anzahl an Prädiktoren

plot(model.bmi, "subset", type=0)

Es sieht so aus, als ob R_adj.² ab 8 Prädiktoren nicht mehr wesentlich ansteigt. Um uns einen visuellen Eindruck zu verschaffen, erzeugen wir als nächstes eine Serie an Perzentilbändern zwischen 5 und 15 Prädiktoren.

# Erzeugt eine Serie an Perzentilplots mit aufsteigender Anzahl von Prädiktoren

plotPercentileSeries(model.bmi, start = 5, end = 15)

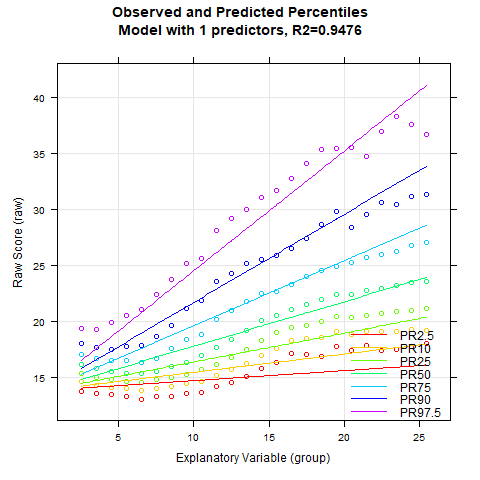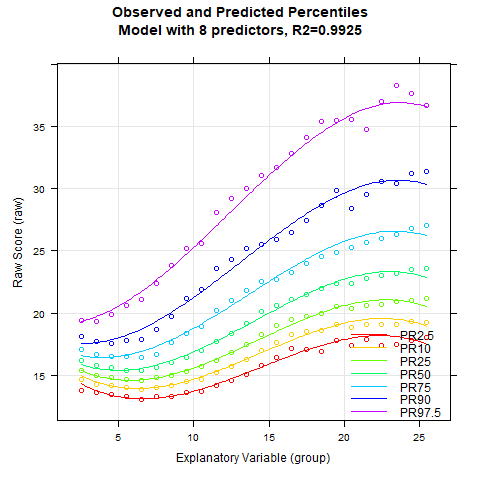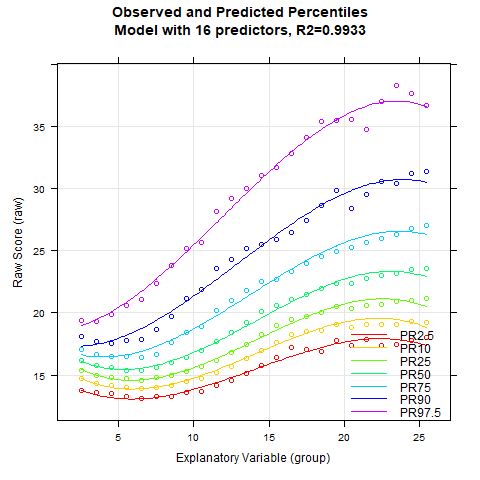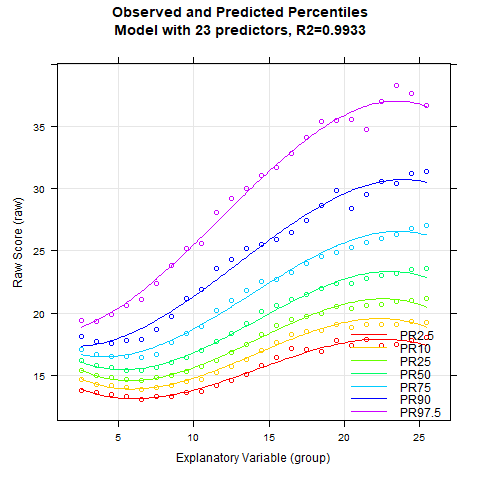
An der Perzentilserie lässt sich erkennen, dass die Schätzung der Perzentilbänder ab etwa 10 Prädiktoren weitgehend stabil bleibt. Auch hier beträgt die Varianzaufklärung gerundet bereits 99.3 %.

Auffällig ist, dass die BMI-Daten einen relativ komplexen Altersverlauf aufweisen. So sinkt der BMI zunächst zumindest in den unteren Perzentillinien vom zweiten bis etwa zum siebten Lebensjahr. In dieser Phase wandelt sich der menschliche Körper also von der kompakten Form eines Babys zu einem länglicheren Körper. Danach steigt der BMI bis etwa zum 23. Lebensjahr kontinuierlich an. Das Modell mit 10 Prädiktoren scheint innerhalb dieses Bereichs ziemlich gut auf die Daten zu passen. Allerdings zeigt unser Modell an, dass bei noch höherem Alter der BMI wieder leicht sinkt. Dieser Effekt ist weder sonderlich plausibel, noch passt er gut auf die Daten. Denn die manifesten Daten sehen eher so aus, als ob der BMI ab diesem Alter weiter steigt oder höchstens konstant bleibt. Bei solch komplexen Altersverläufen kann es helfen, den Parameter t für die Altersanpassung zu erhöhen. Das Maximum liegt bei 6. Bei einem so hohen Wert und der großen Fallzahl von N = 45035 würde der Rechner allerdings extrem lange rechnen. Den Parameter t auf über 5 zu setzen, wird vermutlich auch nur selten vonnöten sein. Wir probieren es also mit t = 5.

model.bmi <- cnorm(raw=CDC$bmi, group=CDC$group, t=5)

Wegen des großen Datensatzes und der hohen Anzahl an Potenzen müssen wir eine Weile auf das Ergebnis warten.

...

Endlich: Das Ergebnis ist da. Es sieht viel besser aus: 99.67 % Varianzaufklärung, allerdings werden jetzt 35 Terme angezeigt. Das ist definitiv zu viel. Wir lassen uns deshalb R_adj.² und die Perzentilplots in Abhängigkeit von der Anzahl an Prädiktoren ausgeben, um nach einem sparsameren Modell zu suchen.

plot(model.bmi, "subset", type=0)
plotPercentileSeries(model.bmi, start = 5, end = 20)

Ab 15 Prädiktoren steigt die Varianzaufklärung kaum noch. Wir suchen deshalb in den Perzentilplots nach einem Modell mit höchstens 15 Prädiktoren, das in den hohen Altersstufen trotzdem einen vernünftigen Verlauf aufweist. Wir werden bei 14 Prädiktoren fündig und erzielen auch hier bereits eine Varianzaufklärung von 99.6 %.

Das sieht sehr gut aus. Das Modell bildet die manifesten Daten jetzt auch in den hohen Altersbereichen nahezu perfekt ab. Wir führen deshalb zur endgültigen Auswahl des Modell eine Neuberechnung durch, bei der wir die Anzahl der Terme auf 14 setzen.

model.bmi <- cnorm(raw=CDC$bmi, group=CDC$group, t=5, terms=14)

Eine andere Möglichkeit der Modellierung hätte bei diesem großen Datensatz übrigens darin bestanden, nicht t hochzusetzen, sondern zwei Altersgruppen zu bilden und diese getrennt zu modellieren, z. B. von 2 bis 12 und von 12 bis 25 Jahren. Noch besser ist es sogar, wenn man bei der Modellierung die Altersbereiche leicht überlappen lässt, also z. B. eine Gruppe von 2 bis 15 und eine von 12 bis 25 bildet. Probieren Sie es doch einmal selbst aus. Für eine solche Gruppenbildung können Sie den folgenden Code verwenden:

# Erzeugt zwei getrennte Altersgruppen

CDC_young <- CDC[CDC$age<=15,]
CDC_old <- CDC[CDC$age>=12,]

3. Modellierung von Reaktions- und Bearbeitungszeiten

Reaktions- oder Bearbeitungszeiten sind in der Regel extrem rechtsschief verteilt. Dies kommt daher, dass Reaktionszeiten nach unten durch 0 begrenzt sind, aber nicht oder kaum nach oben. Häufig werden Reaktions- und Bearbeitungszeiten vor der Weiterverarbeitung einer logarithmischen Transformation unterzogen, um die Daten einer Normalverteilung anzunähern. Dummerweise lässt sich gerade eine solche logarithmische Transformation mit Taylorpolynomen nur schlecht bewerkstelligen. Bei Reaktions- und Bearbeitungszeiten kann es deshalb von Vorteil sein, die Daten vor der Modellierung zunächst einer logarithmischen Transformation zu unterziehen. Wenn die Transformation tatsächlich ihren Dienst tut und die Verteilungen an Normalverteilungen angenähert, dann können die Daten anschließend auch wieder besser mit Taylorpolynomen approximiert werden.

Einen solchen Fall möchten wir Ihnen hier zeigen. In der Aufgabe, die hier verwendet wurde, mussten Kinder zwischen 6 und 12 Jahren so schnell wie möglich auf einen nach links zeigenden Pfeil mit einem linken Tastendruck und auf einen nach rechts zeigenden Pfeil mit einem rechten Tastendruck reagieren. Dabei mussten sie Pfeile ignorieren, die um den Zielpfeil herum eingeblendet wurden. Die Aufgabe erfasst Aufmerksamkeitsprozesse. Jedes Kind absolvierte 100 Durchläufe, über die anschließend gemittelt wurde. Aus urheberrechtlichen Gründen können wir den Datensatz leider nicht in cNORM zur Verfügung stellen.

Mit der Beta-Binomialverteilung lassen sich die Daten nicht modellieren, da es sich um kontinuierliche Rohwerte handelt. Wie wenden deshalb die verteilungsfreie Normierung an, und zwar zunächst auf die untransformierten Reaktionszeiten. Da bei Reaktionszeiten kleinere Werte ein besseres Ergebnis in Bezug auf Aufmerksamkeit bedeuten, wählen wir außerdem in der 'cnorm()'-Funktion 'descend=TRUE'. Dies hat zur Folge, dass niedrige Rohwerte mit hohen Perzentilen verknüpft werden.

# Ermittlung eines Models für die Variable 'raw2' aus dem ADHD-Datensatz

model.ADHD <- cnorm(raw=ADHD$raw2, age=ADHD$age, width=1, descend=TRUE)

Leider erhalten wir nur 97.9 % Varianzaufklärung. Außerdem verläuft die PR2.5-Linie vermutlich zu gerade, die PR97.5-Linie dafür zu gewellt. Wir unterziehen die Rohwerte deshalb einer logarithmischen Transformation und modellieren anschließend noch einmal. Außerdem prüfen wir R_adj² in Abhängigkeit von der Anzahl der Prädiktoren und lassen uns anschließend noch eine Perzentilserie ausdrucken.

# Logarithmische Transformation der Rohwertvariable
# und Neumodellierung

ADHD$lograw2 <- log(ADHD$raw2)
model.ADHDlog <- cnorm(raw=ADHD$lograw2, age=ADHD$age, width=1, descend=TRUE)
plot(model.ADHDlog, "subset", type = 0)
plotPercentileSeries(model.ADHDlog, start = 2, end = 10)

Die Grenze von 99 % Varianzaufklärung erreichen wir leider immer noch nicht, wir kommen ihr aber jetzt schon ein ganzes Stück näher. Außerdem sieht es so aus, als ob ab 6 Prädiktoren keine wesentliche Modellverbesserung mehr zu erreichen ist. Wir schauen uns deshalb das Modell mit 6 Prädiktoren an.

Das Modell sieht gut. Es klärt 98.6 % der Datenvarianz auf. Zwar deutet ein Wert unter 99 % darauf hin, dass wir es mit nur mäßig gut modellierbaren Daten zu tun haben. Im vorliegenden Fall liegt dies allerdings nicht an der gewählten Modellierungsmethode, sondern daran, dass Reaktionszeiten bzw. Bearbeitungsgeschwindigkeiten generell keine sonderlich hohe Reliabilität aufweisen, was sich dann auch bei der Normierung bemerkbar macht. Es bleibt uns also nichts anderes übrig, als uns mit diesem Ergebnis zufrieden zu geben. Um das Modell endgültig auszuwählen, führen wir eine Neuberechnung durch, bei der wir die Anzahl der Terme auf 6 setzen.

model.ADHDlog <- cnorm(raw=ADHD$lograw2, age=ADHD$age, width=1, descend=TRUE, terms=6)

Wenn die Daten vor der Normierung einer logarithmischen Transformation unterzogen werden, dann darf natürlich nicht vergessen werden, diese Transformation bei der Erzeugung von Normtabellen zu berücksichtigen. Auf den in der Tabelle zu einem Normwert ausgegebenen Rohwert muss also die e-Funktion angewandt werden, um endgültige Zuordnungen zwischen mitteleren Reaktionszeiten und Normwerten zu erhalten.

Abschlussbemerkung

Große Datensätze zu modellieren, erinnert bisweilen tatsächlich an die Arbeit von Bildhauern. Man nimmt hier ein bisschen weg und fügt dort ein bisschen hinzu, um letzten Endes ein visuell befriedigendes Ergebnis zu erhalten. In vielen Fällen gibt es kein eindeutiges Richtig oder Falsch. Auch die beste Modellierung kann außerdem aus einem stark unrepräsentativen oder viel zu kleinen Datensatz oder aus einer Skala mit hohem Messfehler keinen guten Test machen. Dummerweise treten die größten Normierungsfehler in der Regel in den extremen (vor allem in den extrem niedrigen) Wertebereichen auf. Dies gilt übrigens nicht nur für cNorm, sondern für alle Normierungsverfahren. Gerade diese Bereiche sind es aber, die in der diagnostischen Praxis die höchste Relevanz besitzen. So entscheidet ein Normwert im niedrigen Bereich nicht selten über Schullaufbahnen, Fördermaßnahmen oder über die Notwendigkeit therapeutischer Versorgung. Testnormierungen stellen deshalb hohe Anforderungen an die Verantwortung, Sorgfalt und Mühe des Testkonstrukteurs oder der Testkonstrukteurin. Wir hoffen, dass wir mit cNORM dazu beitragen können, diese Anforderungen leichter zu erfüllen und die diagnostische Sicherheit damit zu erhöhen.

Anpassung mittels Betabinomial-Verteilung

Grafische Nutzeroberfläche

Copyright © 2018 - 2022 Drs. Alexandra & Wolfgang Lenhard